Introduction to Diffraction Gratings
What are Diffraction Gratings
A diffraction grating is an optical element that divides(disperses) light composed of lots of different wavelengths(e.g., white light) into light components by wavelength. The simplest type of grating is one with a large number of evenly spaced parallel slits. When white light enters the grating, the light components are diffracted at angles that are determined by the respective wavelengths(diffraction). Picking out diffracted (reinforced) light makes it possible to select the required light component. In short, for parallel beams that enter neighboring slits as shown in Fig. 1, light is reinforced when the optical path difference is a multiple of the wavelength. The light from all the slits is reinforced in the same way to produce "diffracted light."
-
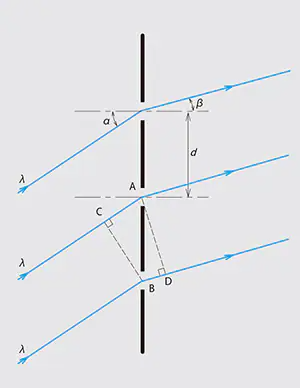
Fig. 1-1 The Principle of Transmission Gratings
-
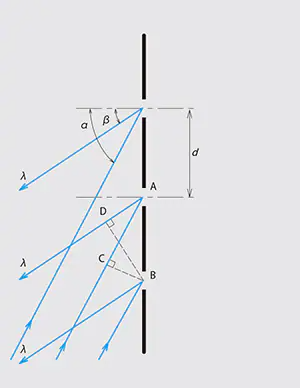
Fig. 1-2 The Principle of Reflection Gratings
The Grating Equations
As shown in Fig.1-1 and Fig.1-2, α is the angle between the incident light and the normal to the grating (the incident angle) and ß is the angle between the diffracted light and the normal to the grating (the diffraction angle), then, they satisfy the following relationship:
as shown in Fig.1-1, in case of transmission grating
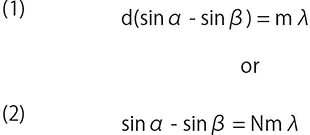
as shown in Fig.1.2 in case of a reflection grating,
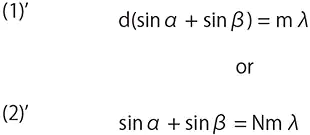
d : Spacing between the slits (the grating period)
N : Number of slits per mm (the groove density, equal to the reciprocal of the grating period)
m : Order of diffraction (m = 0, ± 1, ± 2,...)
λ : Wavelength
It can be seen from this relationship that all components of light corresponding to m = 0 (zero-order light) are radiated in a straight line and so it is not possible to separate the wavelengths with this order. It can also be seen that for m ≠ 0 the diffraction angle ß is different for each wavelength. This is why gratings can be used to separate white light into its constituent wavelengths. The diffraction angle ß also varies with the groove density N and the incident angle α. One point requiring consideration is that, depending on the groove density N, it may not be possible to obtain diffracted light. For example, if the incident angle α = 30° and the groove density N = 2400 grooves/mm, applying the equation to first-order light (i.e., m = +1) with a wavelength λ of 700nm gives sin ß = 1.18, then diffracted light cannot be obtained in this case.
Dispersion
The way in which the diffraction angle λβ behaves when light composed of different wavelengths is directed at a grating is an important point when considering the separation of light into its components. If the incident angle α is regarded as a constant, differentiating both sides of equation (2) with respect to λ gives the following:

Here, dβ/dλ is called the "angular dispersion" and can be used to obtain the change in diffraction angle dβcorresponding to a change in wavelength dλ. Multiplying both sides of equation (3) by the focal distance ƒ for the optical systems gives the following:

When ƒ·dβ = dx, inverting both sides of equation (4) gives the following:
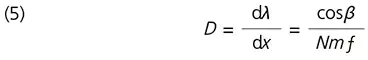
Here, D is called the "reciprocal linear dispersion" and represents the difference in wavelength per unit length on the surface of the exit slit in the optical system. Multiplying D by the slit width gives an indication of the wavelength resolution.





