SHIMADZU Gratings
Toroidal Diffraction Gratings
A toroidal diffraction grating is a sort of concave gratings. The toroidal shape is defined by two curvature radii at each central axis. Toroidal shapes where Rh is a horizontal curvature radius and Rv is a vertical curvature radius. The toroidal shapes are expressed in the following equation.
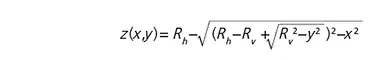
The paraxial focal positions of a toroidal grating in Fig.9 are defined by equations (15) and (16). Here r is the entrance length, r'h is the horizontal focal length, and r'v is the vertical focal length. α and β satisfy the grating equation (2)'.
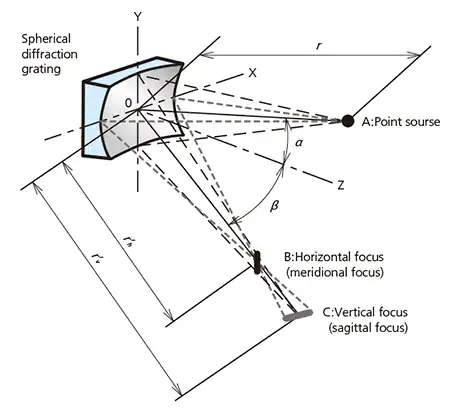
Fig.9 The different focus of the Spherical diffraction grating
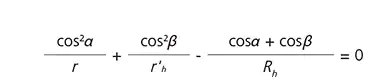
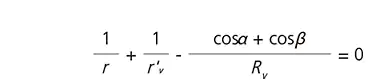
The spherical diffraction gratings are formed on spherical blanks( Rh=Rv ) that has two focal lengths(r'h, r'v ) has astigmatisms, The toroidal diffraction gratings are formed on toroidal (aspheric) blanks( Rh≠Rv ) that can correct astigmatisms.
Choice of a Grating
Selection Chart for Shimadzu Diffraction Gratings
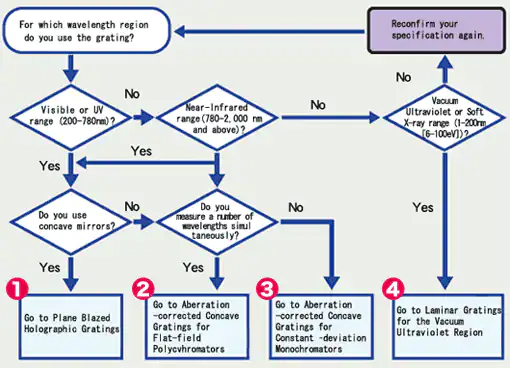
- Go to Plane Blazed Holographic Gratings
- Go to Aberration-corrected Concave Gratings for Flat-field Polychromators
- Go to Aberration-corrected Concave Gratings for Constant-deviation Monochromators
- Go to Laminar Gratings for the Vacuum Ultraviolet Region





